Stochastic Delay Differential Equations: A Comprehensive Approach for Understanding Biosystems with Application to Disease Modelling
Abstract
:1. Introduction
2. General Formulation
2.1. Numerical Scheme for SDDEs
2.1.1. Euler–Maruyama Scheme
2.1.2. Milstein Scheme
| Listing 1. Implementation algorithm. |
| 1. Define the initial condition Y[0] and the time interval [0,T]. 2. Define the time step and the number of time steps N = (T-t_0)/dt 3. Initialize the solution array Y with Y[0] and the Wiener process array W with increments W(t_n). 4. For n = 1 to N do the following: a. Compute the drift term f(t_n,Y(t_n),Y(t_n−tau)) and the diffusion term g(t_n,Y(t_n),Y(t_n−tau)). b. Generate a Wiener increment W(t_n) using a random no generator. c. Compute the approximation Y(t_{n+1}) using the Euler-Maruyama or Milstein formula . d. Append Y(t_{n+1}) to the solution array Y and W(t_n) to the Wiener process array W. 5. Return the solution array Y and the Wiener process array W. |
3. The Evolution of Modelling to SDDEs
3.1. Population Dynamics
3.2. Epidemiology
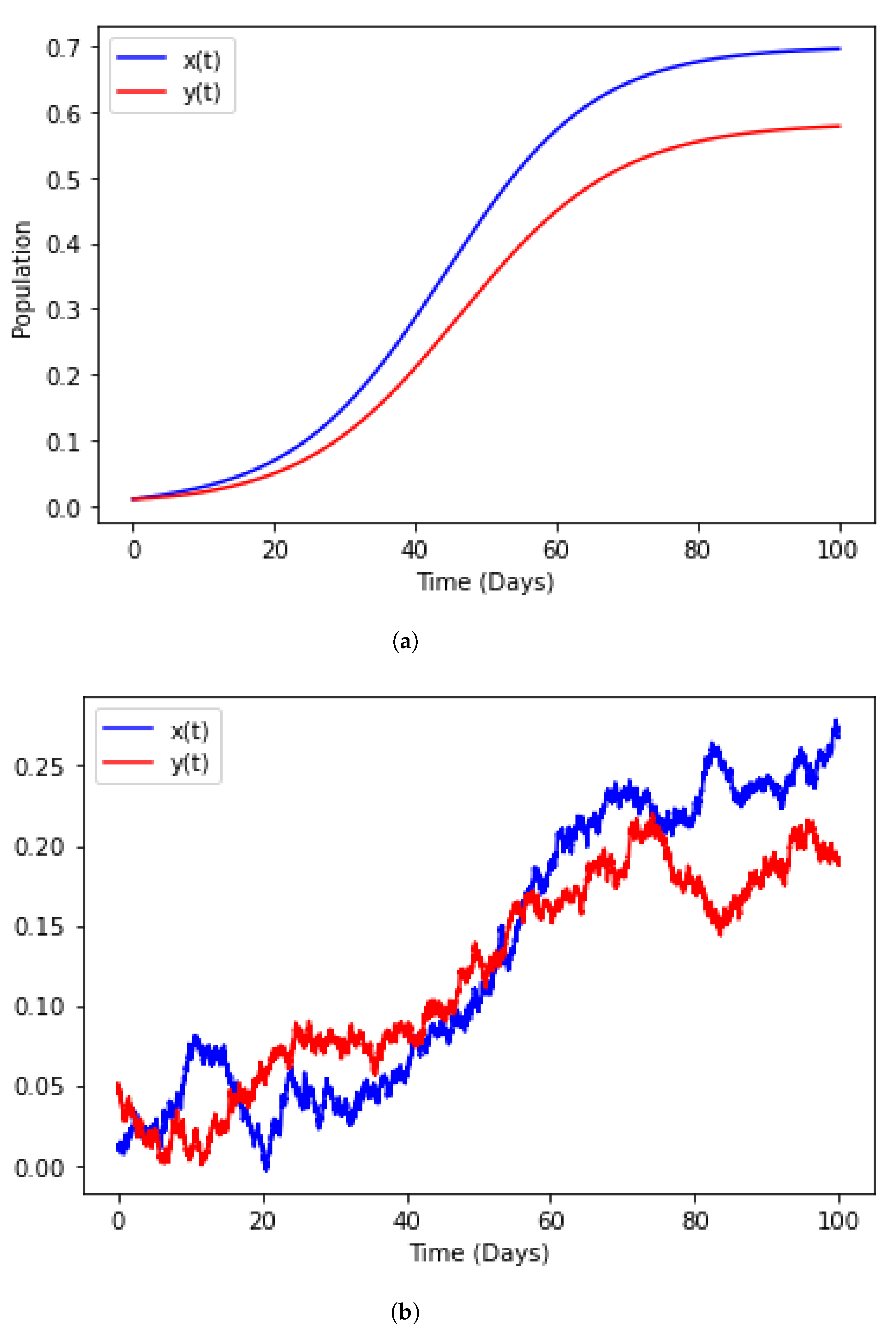
3.3. Ross–Macdonald Malaria Model
4. Numerical Illustration
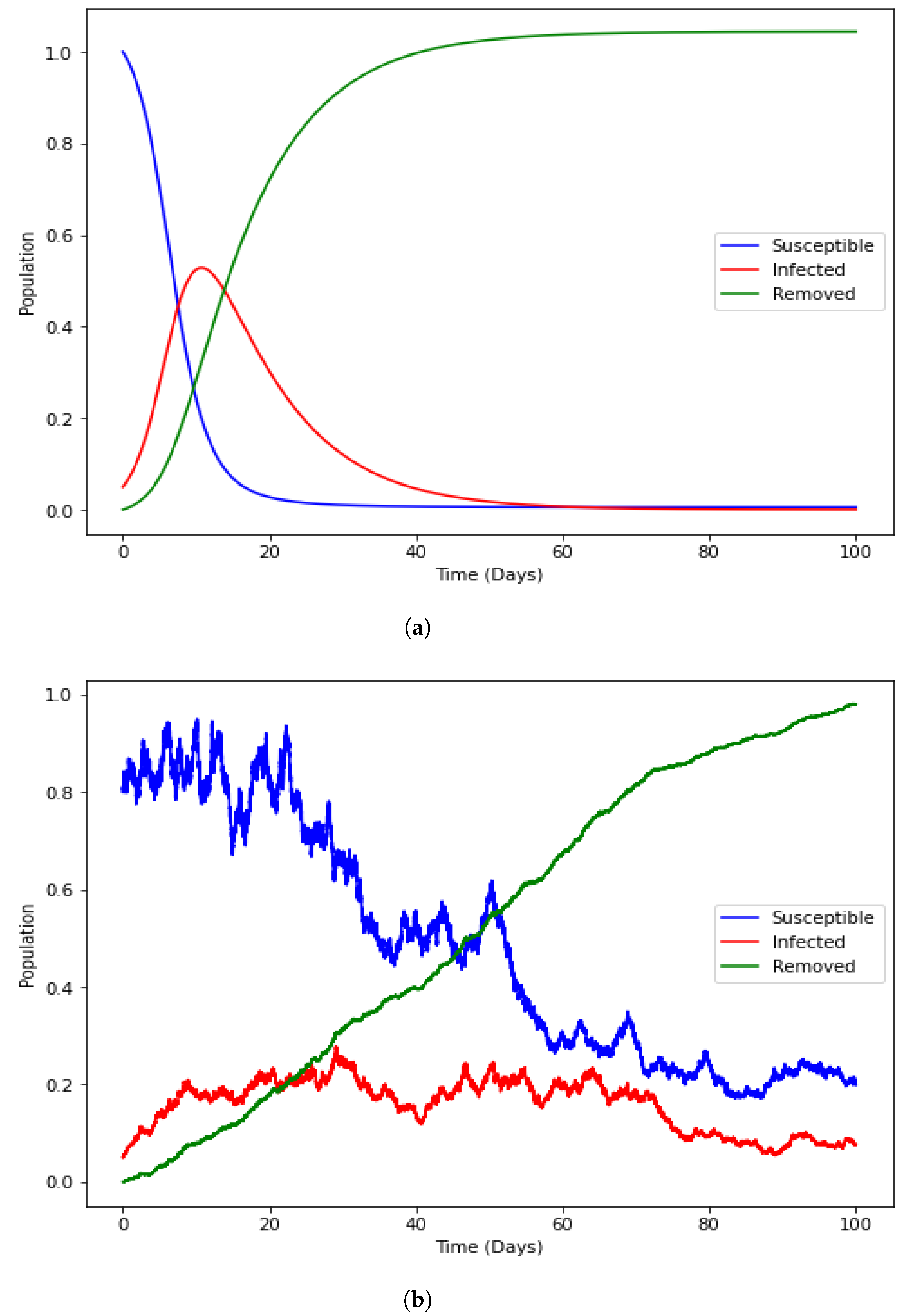
4.1. Positivity of the Solution
4.2. Equilibrium
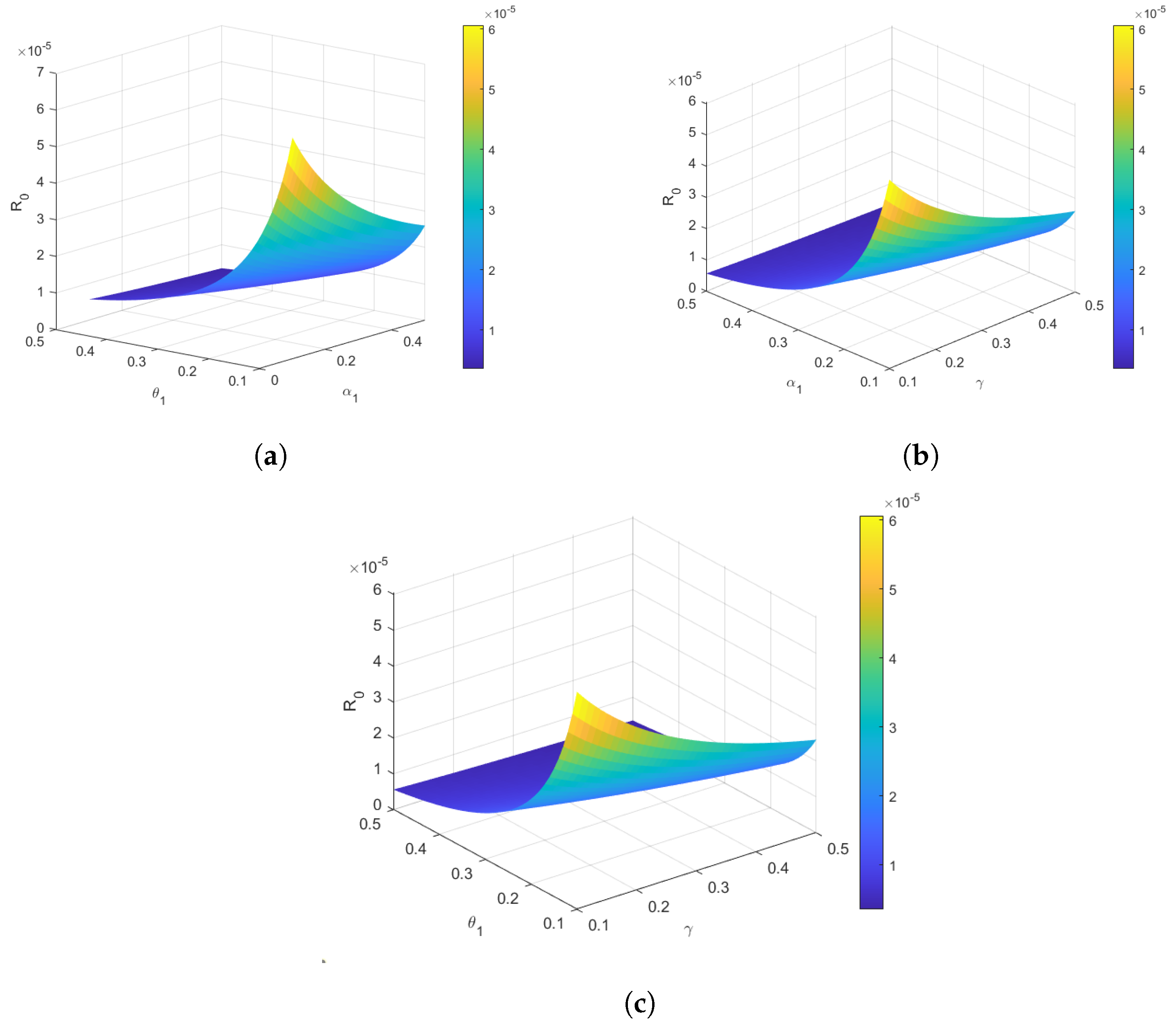
4.3. Reproduction Number
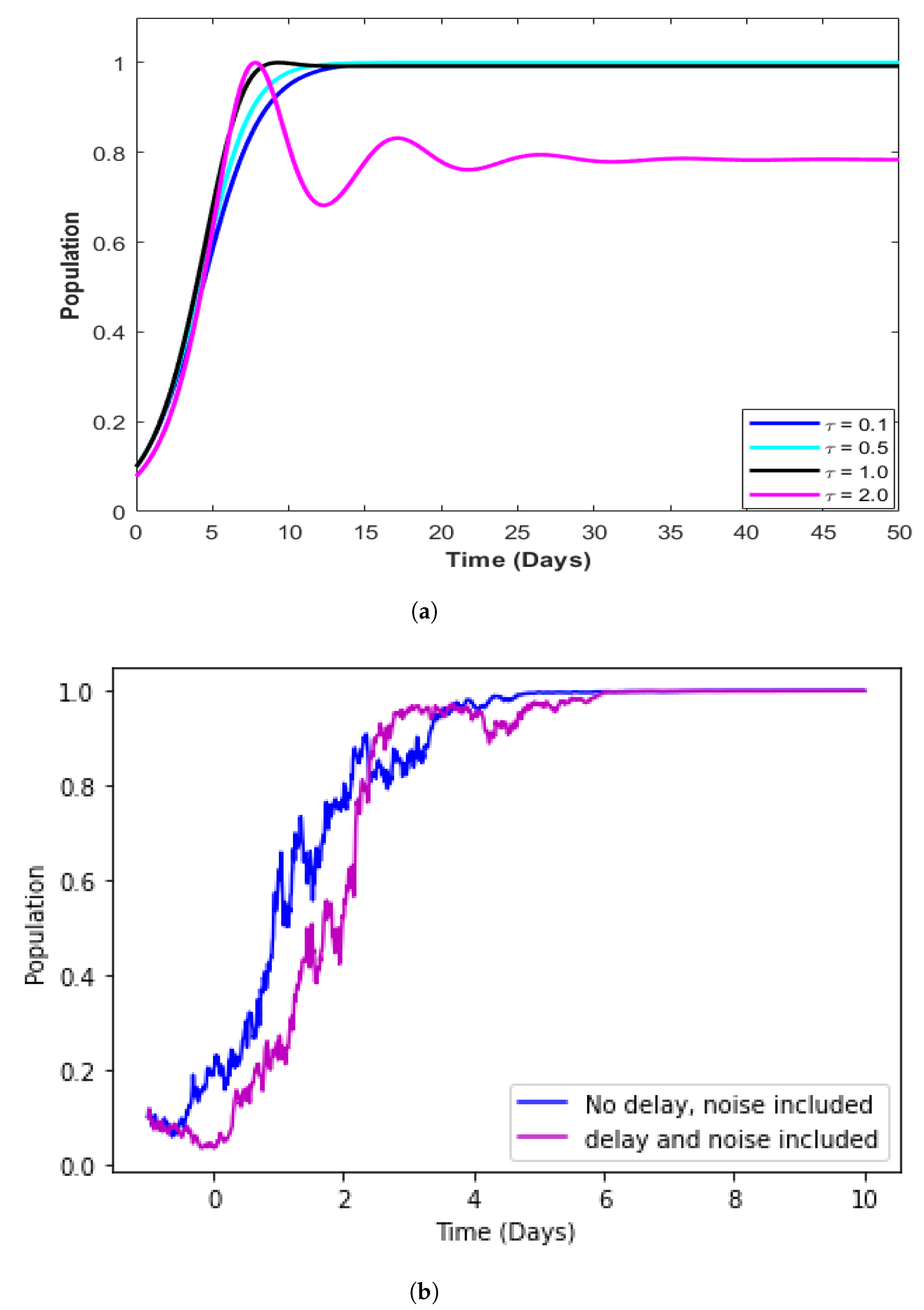
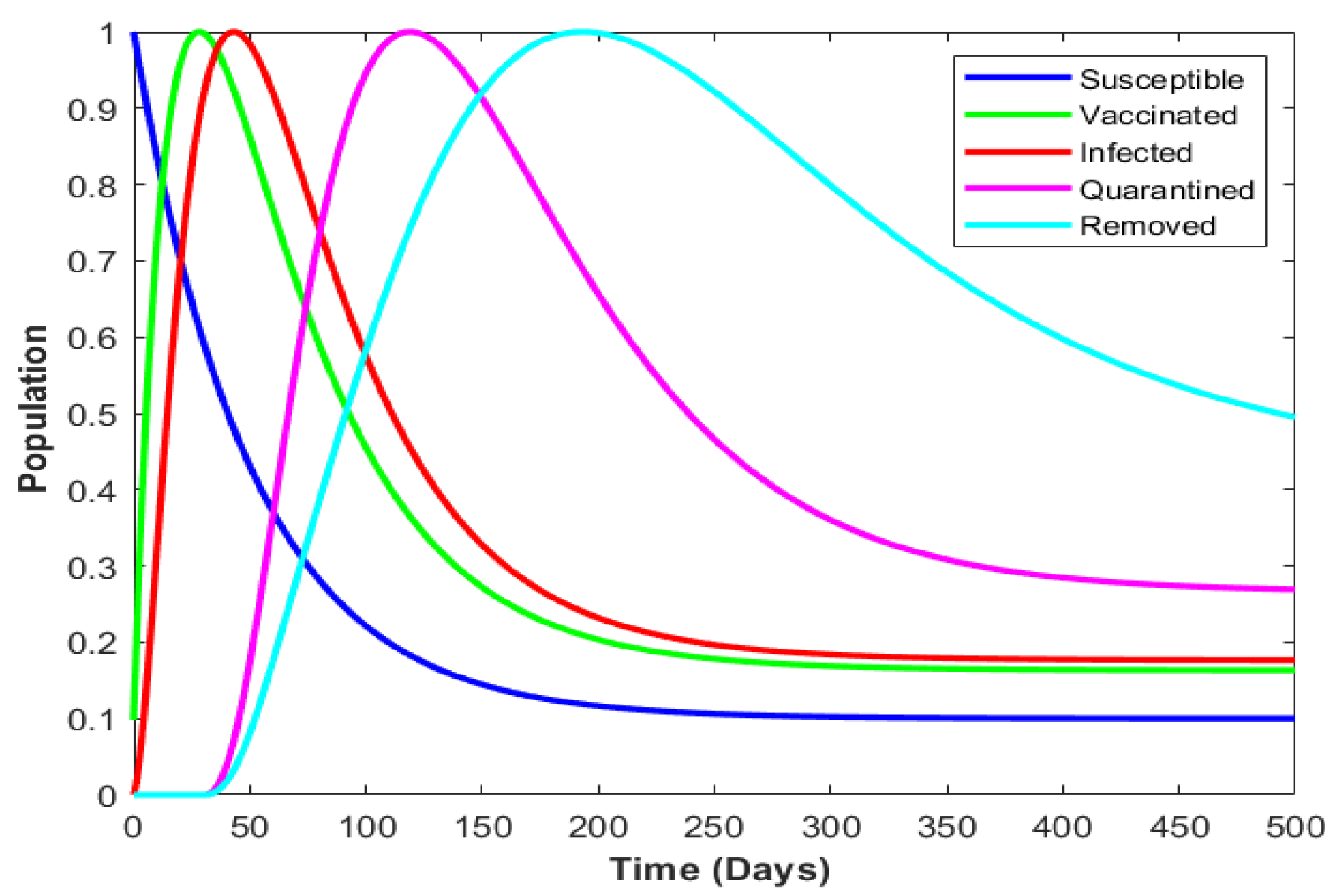
4.4. Numerical Illustration
4.5. Model with Incorporated Delay
4.6. Model with Incorporated Delay and Additive Noise
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kammegne, B.; Oshinubi, K.; Babasola, O.; Peter, O.J.; Longe, O.B.; Ogunrinde, R.B.; Titiloye, E.O.; Abah, R.T.; Demongeot, J. Mathematical Modelling of the Spatial Distribution of a COVID-19 Outbreak with Vaccination Using Diffusion Equation. Pathogens 2023, 12, 88. [Google Scholar] [CrossRef] [PubMed]
- Oshinubi, K.; Peter, O.J.; Addai, E.; Mwizerwa, E.; Babasola, O.; Nwabufo, I.V.; Sane, I.; Adam, U.M.; Adeniji, A.; Agbaje, J.O. Mathematical Modelling of Tuberculosis Outbreak in an East African Country Incorporating Vaccination and Treatment. Computation 2023, 11, 143. [Google Scholar] [CrossRef]
- Buckwar, E. Introduction to the numerical analysis of stochastic delay differential equations. J. Comput. Appl. Math. 2000, 125, 297–307. [Google Scholar] [CrossRef]
- Kloeden, P.E.; Platen, E. A survey of numerical methods for stochastic differential equations. Stoch. Hydrol. Hydraul. 1989, 3, 155–178. [Google Scholar] [CrossRef]
- Higham, D.J.; Mao, X.; Yuan, C. Almost sure and moment exponential stability in the numerical simulation of stochastic differential equations. SIAM J. Numer. Anal. 2007, 45, 592–609. [Google Scholar] [CrossRef]
- Mao, X. Robustness of exponential stability of stochastic differential delay equations. IEEE Trans. Autom. Control 1996, 41, 442–447. [Google Scholar] [CrossRef]
- Bayram, M.; Partal, T.; Orucova Buyukoz, G. Numerical methods for simulation of stochastic differential equations. Adv. Differ. Equ. 2018, 2018, 17. [Google Scholar] [CrossRef]
- Akutsah, F.; Mebawondu, A.A.; Babasola, O.; Pillay, P.; Narain, O.K. D-Iterative Method for Solving A Delay Differential Equation and a Two-Point Second-Order Boundary Value Problems in Banach Spaces. Aust. J. Math. Anal. Appl. 2022, 19, 6. [Google Scholar]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Berlin/Heidelberg, Germany, 2021; pp. 123–141. [Google Scholar]
- Bocharov, G.A.; Rihan, F.A. Numerical modelling in biosciences using delay differential equations. J. Comput. Appl. Math. 2000, 125, 183–199. [Google Scholar] [CrossRef]
- Guillouzic, S.; L’Heureux, I.; Longtin, A. Small delay approximation of stochastic delay differential equations. Phys. Rev. E 1999, 59, 3970. [Google Scholar] [CrossRef]
- Ivanov, A.; Kazmerchuk, Y.; Swishchuk, A. Theory, stochastic stability and applications of stochastic delay differential equations: A survey of results. Differ. Equ. Dynam. Syst. 2003, 11, 55–115. [Google Scholar]
- Cooke, K.L.; Grossman, Z. Discrete delay, distributed delay and stability switches. J. Math. Anal. Appl. 1982, 86, 592–627. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology: I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Benth, F.E.; Di Nunno, G.; Lindstrom, T.; Øksendal, B.; Zhang, T. Stochastic Analysis and Applications: The Abel Symposium 2005; Springer Science & Business Media: Berlin, Germany, 2007; Volume 2. [Google Scholar]
- Milstein, G.N. Numerical Integration of Stochastic Differential Equations; Springer Science & Business Media: Berlin, Germany, 1994; Volume 313. [Google Scholar]
- Kloeden, P.E.; Platen, E.; Kloeden, P.E.; Platen, E. Stochastic Differential Equations; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Saito, Y. Stability analysis of numerical methods for stochastic systems with additive noise. Rev. Econ. Inf. Stud 2008, 8, 119–123. [Google Scholar]
- Mil’shtejn, G. Approximate integration of stochastic differential equations. Theory Probab. Its Appl. 1975, 19, 557–562. [Google Scholar] [CrossRef]
- May, R.M. Simple mathematical models with very complicated dynamics. Nature 1976, 261, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Hutchinson, G.E. Circular causal systems in ecology. Ann. N. Y. Acad. Sci 1948, 50, 221–246. [Google Scholar] [CrossRef]
- Golec, J.; Sathananthan, S. Stability analysis of a stochastic logistic model. Math. Comput. Model. 2003, 38, 585–593. [Google Scholar] [CrossRef]
- Silva, C.J.; Maurer, H.; Torres, D.F. Optimal control of a Tuberculosis model with state and control delays. Math. Biosci. Eng. 2016, 14, 321–337. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Y.; Kundu, S.; Song, Z.; Zhang, Z. Dynamics of an SIR epidemic model incorporating time delay and convex incidence rate. Results Phys. 2022, 32, 105025. [Google Scholar] [CrossRef]
- Babasola, O.; Kayode, O.; Peter, O.J.; Onwuegbuche, F.C.; Oguntolu, F.A. Time-delayed modelling of the COVID-19 dynamics with a convex incidence rate. Inform. Med. Unlocked 2022, 35, 101124. [Google Scholar] [CrossRef]
- Tipsri, S.; Chinviriyasit, W. The effect of time delay on the dynamics of an SEIR model with nonlinear incidence. Chaos Solitons Fractals 2015, 75, 153–172. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-differential equation model of HIV infection of CD4+ T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Nelson, P.W.; Perelson, A.S. Mathematical analysis of delay differential equation models of HIV-1 infection. Math. Biosci. 2002, 179, 73–94. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.L.; Battle, K.E.; Hay, S.I.; Barker, C.M.; Scott, T.W.; McKenzie, F.E. Ross, Macdonald, and a theory for the dynamics and control of mosquito-transmitted pathogens. PLoS Pathog. 2012, 8, e1002588. [Google Scholar] [CrossRef] [PubMed]
- Aron, J.L.; May, R.M. The population dynamics of malaria. The Population Dynamics of Infectious Diseases: Theory and Applications; Springer: Boston, MA, USA, 1982; pp. 139–179. [Google Scholar]
- Ruan, S.; Xiao, D.; Beier, J.C. On the delayed Ross–Macdonald model for malaria transmission. Bull. Math. Biol. 2008, 70, 1098–1114. [Google Scholar] [CrossRef]
- Fosu, G.O.; Akweittey, E.; Adu-Sackey, A. Next-generation matrices and basic reproductive numbers for all phases of the Coronavirus disease. Open J. Math. Sci. 2020, 4, 261–272. [Google Scholar] [CrossRef]


| Parameter | Description |
|---|---|
| Susceptible population at time t. This is the group of individuals who are not infected but are at risk of becoming infected. | |
| Vaccinated population at time t which represents individuals who have been vaccinated against the disease. | |
| Infectious population at time t. The group of individuals currently infected and capable of spreading the disease. | |
| Quarantined population at time t. Individuals who are quarantined due to infection. | |
| Recovered population at time t. Includes individuals who have recovered from the disease and are no longer infectious. | |
| Recruitment rate of the susceptible population, i.e., the rate at which individuals enter the susceptible group. | |
| Transmission rate of the disease which is the rate at which susceptible individuals become infected when they come into contact with infectious individuals. | |
| Time delay indicating that newly infected individuals do not become infectious immediately but after a delay of time units. | |
| Recovery rate, i.e., the rate at which infected individuals recover and move to the recovered compartment. | |
| Rate at which susceptible individuals become vaccinated. | |
| Rate at which infected individuals are placed in quarantine. | |
| Rate at which the quarantined individuals are recovered. | |
| Rate at which individuals in quarantine transition to the recovered compartment. | |
| Represent the level of fluctuation within each model compartment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Babasola, O.; Omondi, E.O.; Oshinubi, K.; Imbusi, N.M. Stochastic Delay Differential Equations: A Comprehensive Approach for Understanding Biosystems with Application to Disease Modelling. AppliedMath 2023, 3, 702-721. https://doi.org/10.3390/appliedmath3040037
Babasola O, Omondi EO, Oshinubi K, Imbusi NM. Stochastic Delay Differential Equations: A Comprehensive Approach for Understanding Biosystems with Application to Disease Modelling. AppliedMath. 2023; 3(4):702-721. https://doi.org/10.3390/appliedmath3040037
Chicago/Turabian StyleBabasola, Oluwatosin, Evans Otieno Omondi, Kayode Oshinubi, and Nancy Matendechere Imbusi. 2023. "Stochastic Delay Differential Equations: A Comprehensive Approach for Understanding Biosystems with Application to Disease Modelling" AppliedMath 3, no. 4: 702-721. https://doi.org/10.3390/appliedmath3040037
APA StyleBabasola, O., Omondi, E. O., Oshinubi, K., & Imbusi, N. M. (2023). Stochastic Delay Differential Equations: A Comprehensive Approach for Understanding Biosystems with Application to Disease Modelling. AppliedMath, 3(4), 702-721. https://doi.org/10.3390/appliedmath3040037







